公開日：12/05/2018
    シェア：

    GoogleAIの勉強：4時間目「損失を減らす」③

    　 4時間目の「損失を減らす」はなかなかボリュームがあります。雰囲気がわかってしまえばなんてことはないんですが、つかめないと何個とかがチンプンカンプンです。

    さて、今回は「損失を減らす」の中の「勾配降下」です。前回の「反復アプローチ」では「いろいろ試しながら答えに近づく」という考え方を学びましたが、今回はそれをグラフとして見ていくことになります。

    勾配降下

    では、早速グラフをみていきましょう。
    反復アプローチで使ったこちらのグラフ―。

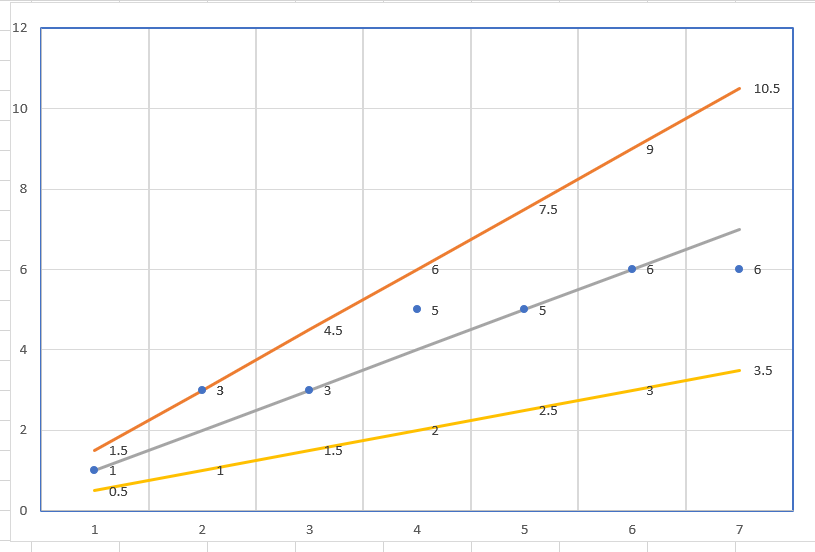
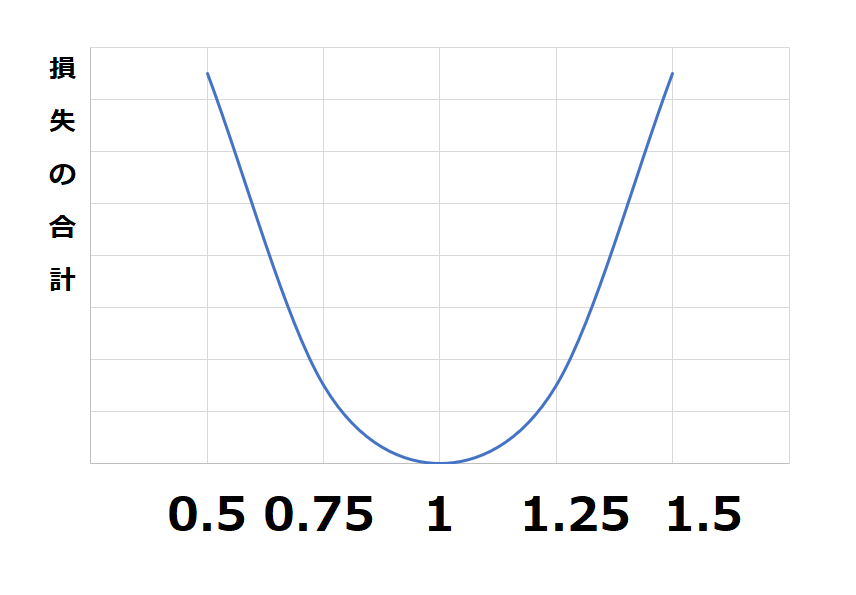
    傾きは１（グレーの線）が理想に近い（損失が少ない）というのは前回の時間に知ることができました。



    さて、傾きが1.5だったり0.5だった場合、損失の合計は大きくなります。
    では、0.25や1.75は？と、ひとつずつ計算するのは大変なので、グラフにしてみました。
    こんな感じのお椀型になりました。これだけではわかりにくいので、それぞれの凡例を入れてみます。
    これだけを見れば一発で「なんだ。傾きは「1」じゃないか」とすぐに分かるわけですが、実際はこの青い線がわからないので、計算をしていかないといけないわけです。

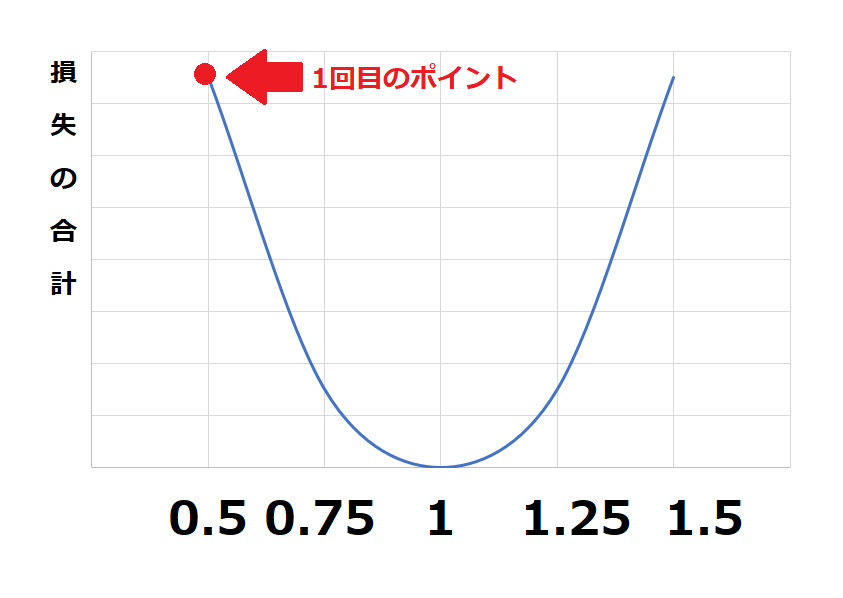
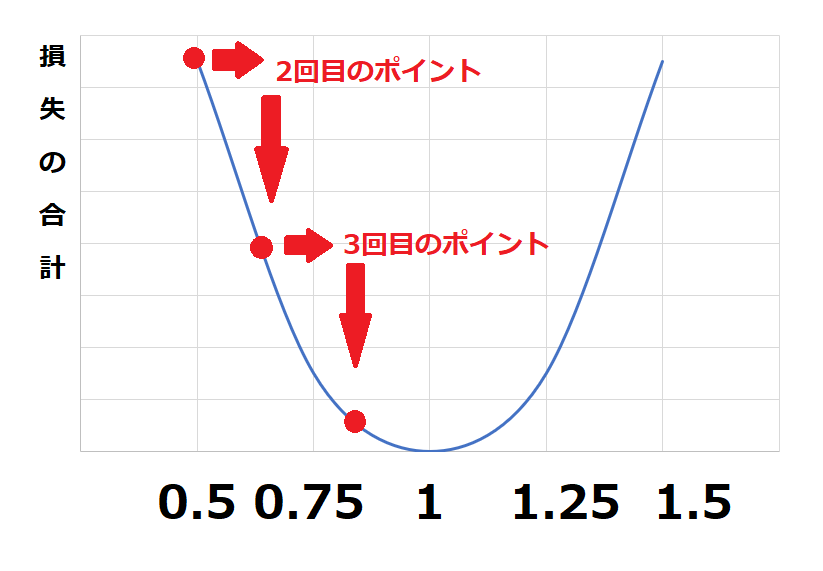
    機械学習では最初にあるポイントで計算をします。
    ここでの損失合計を見るとまだまだ大きい（グラフの高い位置）にあることがわかりますね、
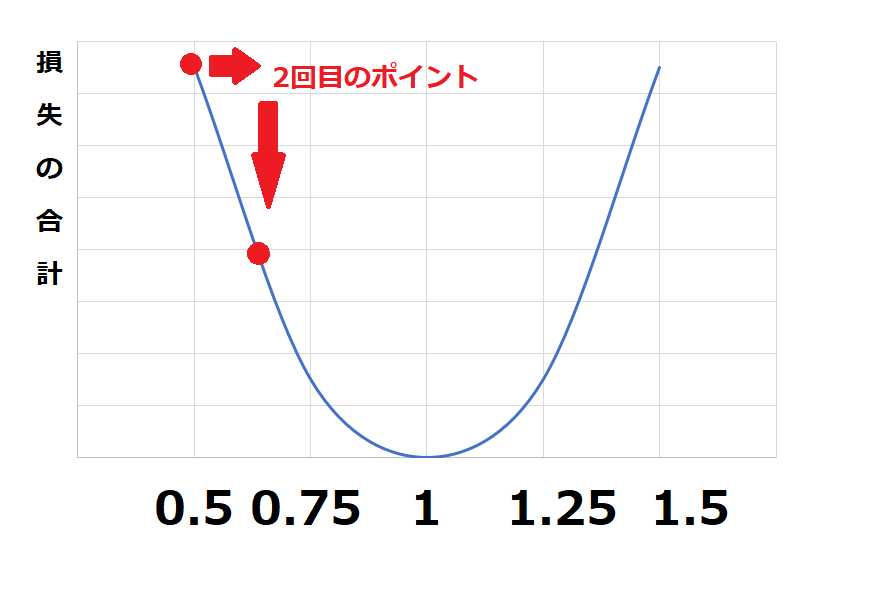
    続いて、一定量右に移動して再度検証してみましょう・
    損失合計が小さく（グラフの位置が低く）なってきました。これを繰り返して、損失の合計が一番低いポイントを探していくことが理解できればこの時間はクリアです。

    ここで気づいた方も多いと思いますが、上のX軸の「0.5」と「1.5」はそれぞれオレンジの線と黄色の線の損失の合計になります。
    理想の線から遠くなれば損失も大きくなるということですね。