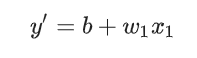GoogleAIの勉強:3時間目「MLへの降順」November 16 2018
GoogleAIの勉強:3時間目「MLへの降順」November 16 2018 GoogleAIの勉強:4時間目「損失を減らす」③December 05 2018
GoogleAIの勉強:4時間目「損失を減らす」③December 05 2018 【Bardに聞いてみた】Googleの検索で上位に来るブログの書き方June 30 2023
【Bardに聞いてみた】Googleの検索で上位に来るブログの書き方June 30 2023 GoogleAIの勉強:コース選択November 12 2018
GoogleAIの勉強:コース選択November 12 2018
公開日:11/16/2018
シェア:Tweet
答え:
全体として誤差は小さくしていきたいところですね。
シェア:Tweet
GoogleAIの勉強:3時間目「MLへの降順」
GoogleAIの勉強も3時間目になりました。今回のタイトルは「MLへの降順」ということで「線形回帰」についても学ぶうです。線形回帰は、一組の点に最もよく合う直線または超平面を見つける方法です。このモジュールは、線形回帰への機械学習アプローチの基礎を築く前に、線形回帰を直感的に調べます。
(出典:https://developers.google.com/machine-learning/crash-course/descending-into-ml/video-lecture)
ということですが、初耳の人にはなんのことだかさっぱりわかりません。詳しくは「統計学」の「線形回帰」を調べてみてください。MLへの降順
では、改めて今回のビデオを見てみましょう。
 |
| 出典:https://developers.google.com/machine-learning/crash-course/descending-into-ml/video-lecture |
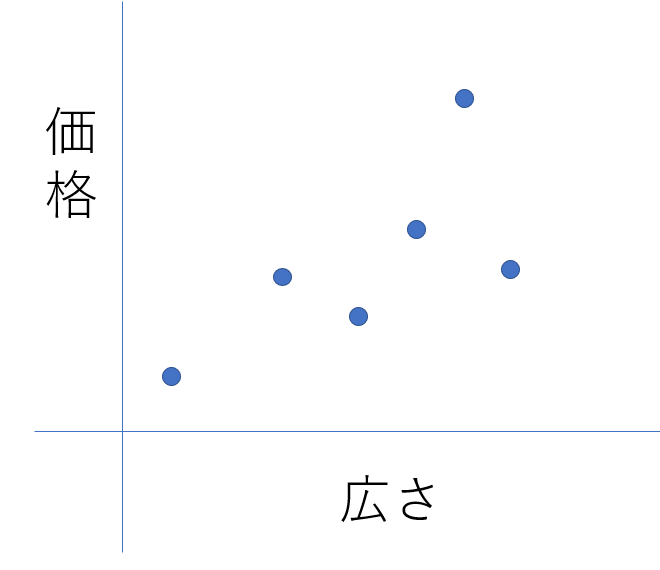
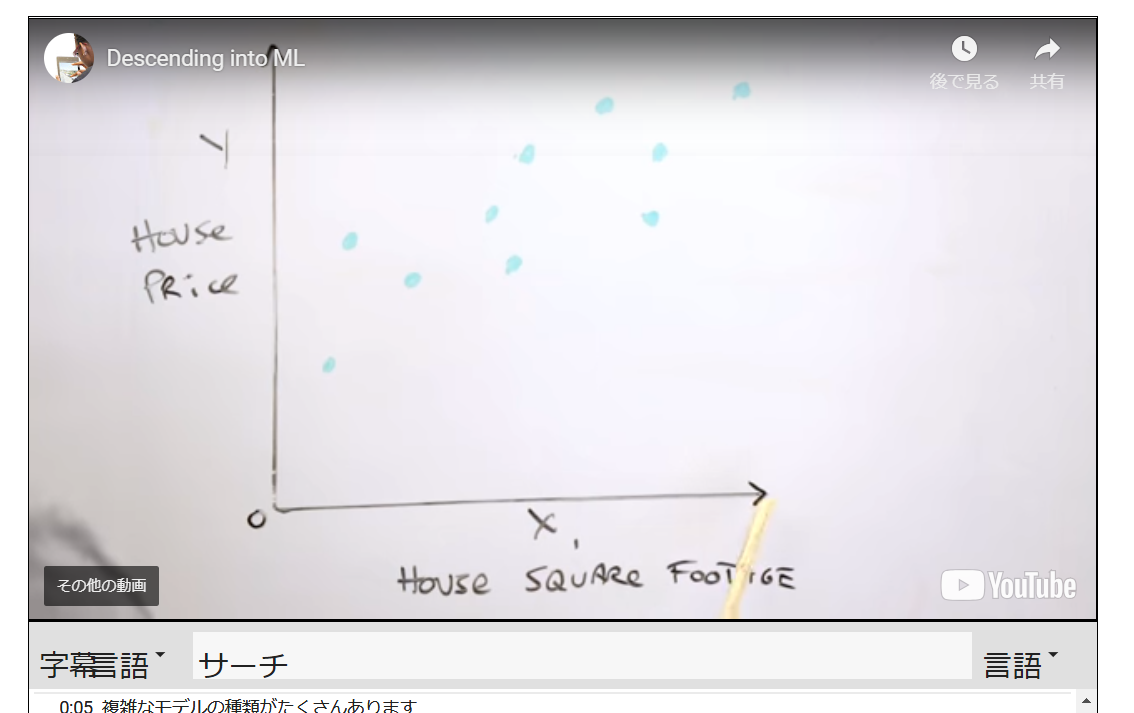
まず最初の例として「家の広さ(X軸)」から「家の価格(Y軸)」を予想するとします。
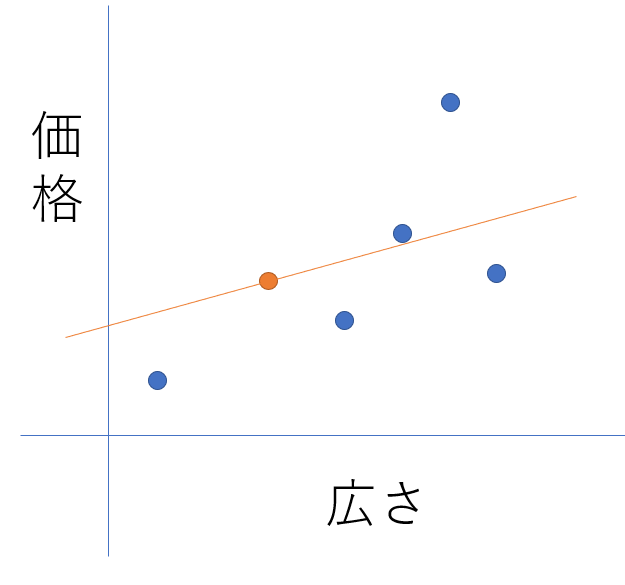
続いて、オレンジ丸を基準にして広さから価格を導く場合のグラフを入れてみます。
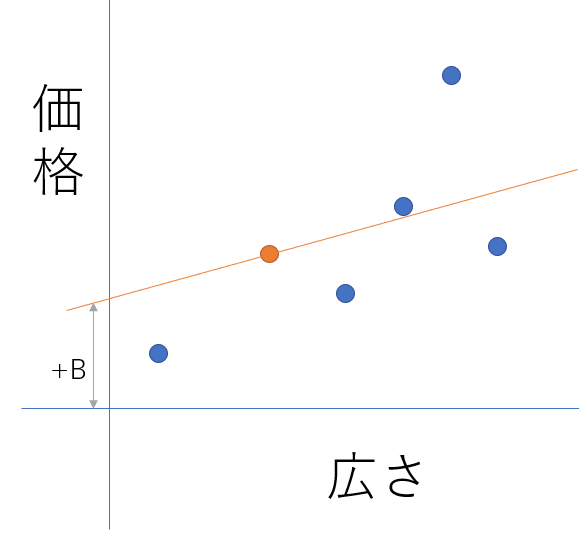
この場合の四季はY=WX+Bとなります。Wは傾きですがこれは機械学習の中で導いてくのかな・・・?+Bは大丈夫ですね。
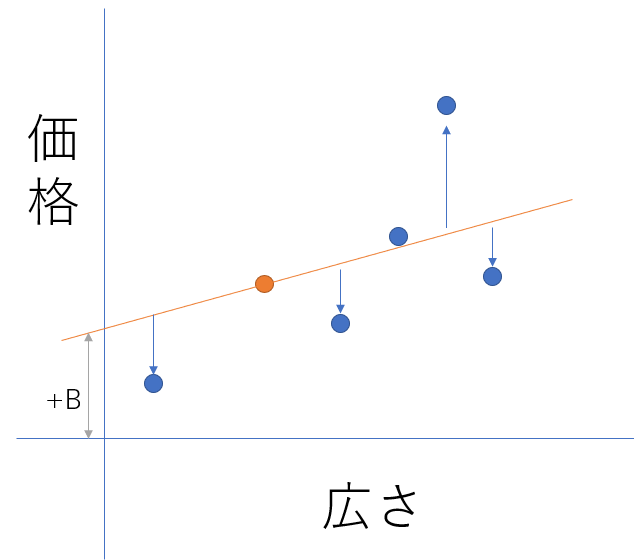
ここで「損失の概念」の説明がはじまります。オレンジの線上が予測値になりますが、残念ながら、点は上下にばらけています。
この差が「損失」というわけですが、これは小さいに越したことはないわけですね。
ちなみに世の中には便利な「損失関数」と言うものが存在しており。機械学習では「平均二乗誤差(MSE)」を使うことが多いそうです。Google検索などすると難しい式や解説がたくさんでてきますが、このあとの内容などを踏まえると
((1個目の点と予測値の差の2乗)+(2個目の点と予測値の差の2乗)+(n個目の点と予測値の差の2乗))/(点の個数)
で出すことができ、この数字は小さい方が良いみたいです。
((1個目の点と予測値の差の2乗)+(2個目の点と予測値の差の2乗)+(n個目の点と予測値の差の2乗))/(点の個数)
で出すことができ、この数字は小さい方が良いみたいです。
わかるようなわかならいような・・・整理するのに次のページを見てみます。
その関係をグラフにすると次のようになるみたいです。
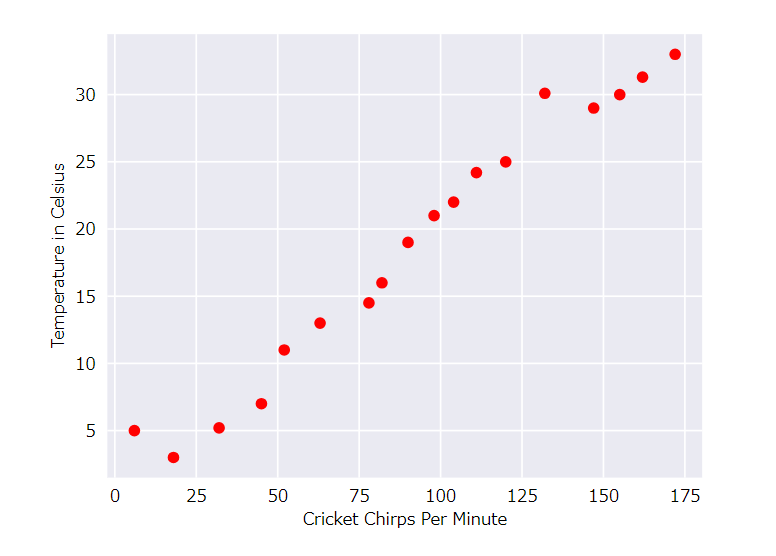 |
| 出典:https://developers.google.com/machine-learning/crash-course/descending-into-ml/linear-regression |
ここに各点を近似値線をくわえてみます。
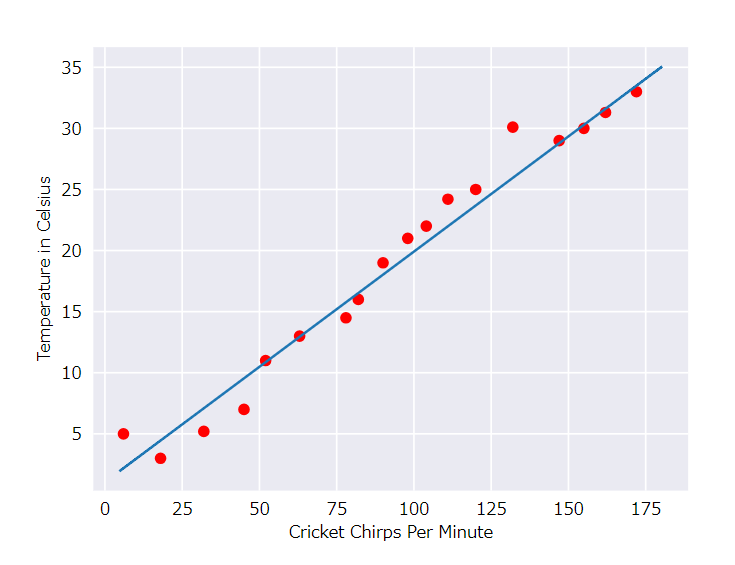 |
| 出典:https://developers.google.com/machine-learning/crash-course/descending-into-ml/linear-regression |
これを式にしてみると
y=mx+b
で表すことができます。
ちなみに機械学習では
で表わすとのことです。実際。wとxはいろいろな要素が入ってくるので、より正確にするためには
と、なるのだとか・・・これはガッチリ統計学なので、勉強していない人には難易度高めです。僕も現段階であまりピンと来ていませんが、まずは雰囲気を掴んでおきたいと思います。
訓練と喪失
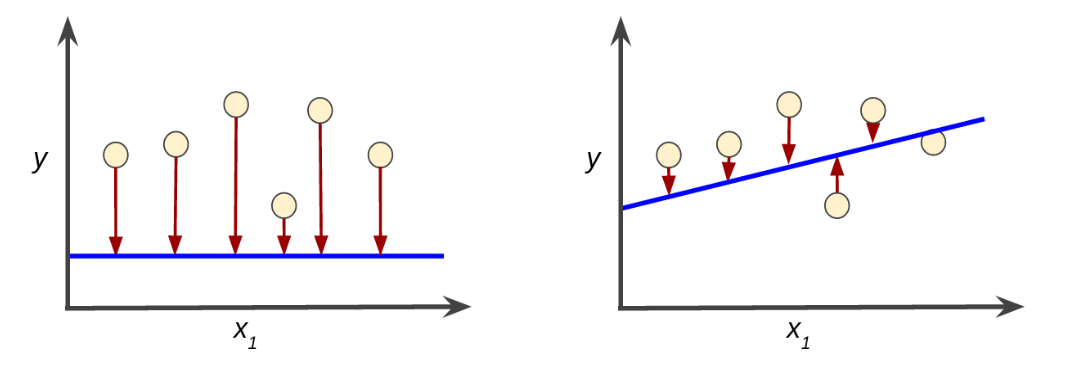
続いて、わからないものをより難題にしていきます。ビデオのときに「損失」について触れていましたが、予測値と実際の差は「損失」になります。
 |
| 出典:https://developers.google.com/machine-learning/crash-course/descending-into-ml/training-and-loss |
例えば上の図で、左側は青線(予測)と実際の点の差が大きいですよね。右の図は少なくなっています。この差を少なくしていくのが「訓練」です。
さて、損失は二乗損失という計算方法で導くことができます。詳しい説明は省略しますが。あくまで機械学習では一般的に使用されいるだけで、実用的な損失関数というわけでもなく、あらゆる状況で最良の損失関数でもありません。とのことでした。
トレーニング
 |
| 出典:https://developers.google.com/machine-learning/crash-course/descending-into-ml/check-your-understanding |
問題
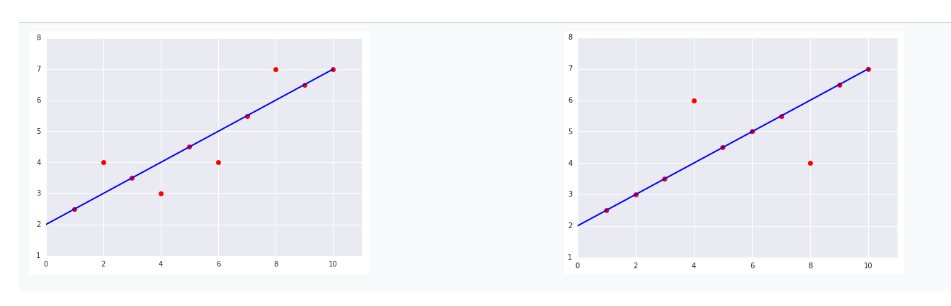
平均二乗誤差(MSE)が高いのは左右どちらのグラフか?答え:
左のグラフ:
誤り・・・ライン上にある6つの例では、合計損失は0になります。ライン上にない4つの例は、それほど遠く離れているわけではないので、オフセットを二乗しても依然として低い値が得られます。
((0*0)+(1*1)+(0*0)+(1*1)+(0*0)+(1*1)+(0*0)+(1*1)+(0*0)+(0*0))/10=0.4
右のグラフ:
正解・・・ライン上の8つの例では、合計損失は0になります。ただし、2つのポイントだけがラインから外れていますが、両方のポイントは、アウトリライアポイントの左の図の2倍です。二乗損失はこれらの差を増幅するので、オフセットが2の場合、オフセットの4倍の損失が発生します。
式
((0*0)+(0*0)+(0*0)+(2*2)+(0*0)+(0*0)+(0*0)+(2*2)+(0*0)+(0*0))/10=0.8
(出典:https://developers.google.com/machine-learning/crash-course/descending-into-ml/check-your-understanding)
全体として誤差は小さくしていきたいところですね。
関連記事
統計情報
126713